Основные операции > Дифференцирование > Многоточечные аппроксимации   

До сих пор для расчета разностных производных применялись двухточечные конечные разности. Однако, порядок аппроксимации можно существенно улучшить, если задействовать большее количество точек, в которых рассчитывается f(x₀). Объем компьютерных вычислений при этом, конечно, возрастет, но и точность численного дифференцирования улучшится.
Чтобы получить многоточечные разностные аппроксимации производной, следует действовать точно так же, как и раньше (см. разд. о погрешностях). Вдобавок к трем точкам: x=x₀-D, x=x₀ и x=x₀+D выберем дополнительные точки аргумента x, например: x=x₀-2D и x=x₀+2D . Подставим эти значения x в разложение Тейлора

с тем, чтобы можно выразить через f (x₀-2D), f (x₀+2D ) и слагаемые, содержащие множитель D² и D³. Полученная после приведения подобных слагаемых формула будет выглядеть следующим образом:

Это - пятиточечная аппроксимация 1-й производной. То, что в ней присутствуют значения f(x) лишь в 4-х точках не должно смущать читателя. Просто оказалось, что f(x₀) входит в нее с множителем 0.

Аналогично можно получить и семиточечную аппроксимацию 1-й производной:

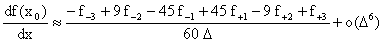
Для краткости, в данной формуле мы обозначили символом f_±D значение функции f(x) в точках, отстоящих влево или вправо от x0 на расстояние, кратное D.
Аналогичным образом можно получить формулы и для производных высших порядков. Следует записать разложение Тейлора с точностью до слагаемых, содержащих нужную производную, а затем подставить в него соответствующие разностные формулы для низших производных. Однако надо учесть, что следует обеспечить надлежащий порядок точности, подставляя в ряд Тейлора соответствующие многоточечные аппроксимации низших производных.