Бифуркации в динамических системах

Анализ фазовых портретов, т.е. решений системы ОДУ, получающихся при выборе всевозможных начальных условий,  является важнейшей задачей исследования динамических систем. При этом следует иметь в виду, что, как правило, имеется некоторая зависимость системы ОДУ, представляющей динамическую систему, от некоторого параметра (параметров). Задача зависимости фазового портрета (в частности, расположения аттракторов на фазовой плоскости)  от параметра модели представляет особый интерес. При отсутствии особенности при плавном изменении параметра модели происходит простое перемещение аттракторов по фазовой плоскости (без изменения типов и количества аттракторов). Критическое сочетание параметров, при которых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации.

Поясним понятие бифуркации на примере динамической системы Лоренца, зависящей от параметра r и нескольких дополнительных параметров. Наиболее интересное ее решение в виде странного аттрактора появляется только при некоторых сочетаниях параметров, в частности, при r~1. При r~10 аттрактором системы Лоренца является фокус. Перестройка типа фазового портрета происходит в области промежуточных r, когда фокус теряет устойчивость, а вместо него появляется странный аттрактор. Заметим, что физический смысл бифуркации в модели Лоренца, согласно современным представлениям, описывает переход ламинарного движения жидкости к турбулентному

Для надежного исследования фазового портрета необходимо решить систему ОДУ большое количество раз с самыми разными начальными условиями (и, возможно, с разным набором параметров модели), чтобы посмотреть, к каким аттракторам сходятся различные траектории. В качестве примера приведем решение системы уравнений автокаталитической химической реакции с диффузией. Эта модель, называемая моделью брюсселятора, предложена в 1968 г. Лефевром и Пригожиным. Неизвестные функции отражают динамику концентрации промежуточных продуктов некоторой реальной химической реакции. Параметр модели B равен исходной концентрации катализатора.

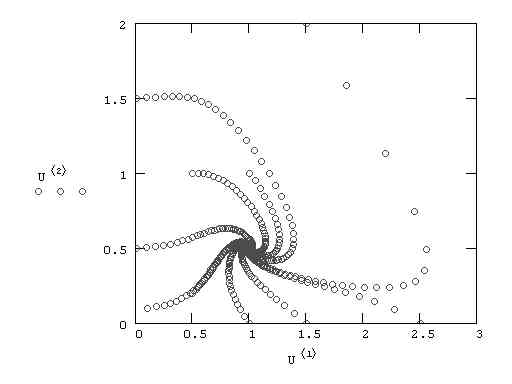
Рис. 1. Фазовый портрет брюсселятора при B=0.5
Как видно из рис.1, все траектории, вышедшие из разных точек, асимптотически стремятся к одному и тому же аттрактору (1,0.5). Из теории динамических систем нам известно, что такой аттрактор называется узлом. (с узлом мы уже встречались ранее) Конечно, в общем случае при анализе фазового портрета желательно "прощупать" большее число траекторий, задавая более широкий диапазон начальных условий. Не исключено, что в других областях фазовой плоскости траектории будут сходиться к другим аттракторам.
Эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром B. При его увеличении узел будет сначала постепенно смещаться в точку с координатами (1,B), пока не достигнет бифуркационного значения B=2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла, т.е. вхождению в режим автоколебаний.  При дальнейшем увеличении B, происходит лишь количественное изменение параметров этого цикла. Решение, полученное при B=2.5, показано на рис.2. 

 

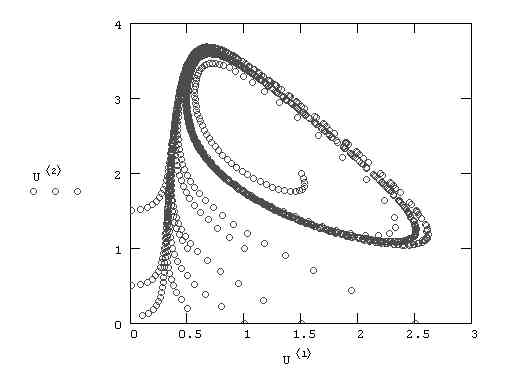
Рис. 2. Фазовый портрет брюсселятора при B=2.5