Модель осциллятора

Рассмотрим уравнение колебаний маятника в поле тяжести. В общем (нелинейном) случае возвращающая сила пропорциональна  - угол отклонения от положения равновесия (вертикальной прямой).

Это уравнение учитывает эффект затухания колебаний с коэффициентом Gamma.

ОДУ гармонического осциллятора описывает колебания маятника при предположении, что их амплитуда мала. В таком случае sin(x)~ x, и уравнение упрощается, становясь линейным. Приведем численное решение ОДУ гармонического осциллятора с конкретными парамерами (рис.1):

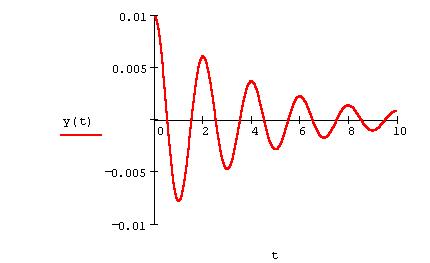
Рис.1. График решения (сверху) и фазовый портрет (снизу) линейного уравнения осциллятора

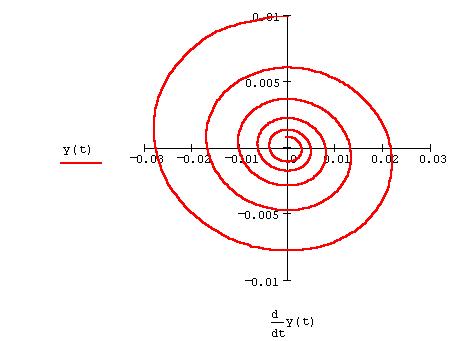
Решением уравнения линейного осциллятора являются затухающие гармонические (синусоидальные) колебания. Фазовый портрет состоит из единственной особой точки (0,0) типа устойчивого фокуса. Если коэффициент затухания положить равным нулю, то колебания будут продолжаться вечно, а особая точка (0,0) станет центром, что переведет ОДУ в разряд негрубых динамических систем.

Если численно решить исходное (нелинейное) уравнение, то колебания будут иметь немного другую (несинусоидальную форму). На рис.2 приведен пример компьютерных расчетов для случая отсутствия затухания. Как Вы видите, особая точка (0,0) является центром, а колебания являются негрубыми (т.е. существенно зависящими от начальных условий). График решения на фазовой плоскости не является эллипсом (что говорит о нелинейности осциллятора). Чем меньше мы будем выбирать амплитуду колебаний (т.е. начальные условия), тем меньше будет проявляться нелинейность (поэтому-то малые колебания маятника можно считать гармоническими).
 
Рис.2.Решение уравнения ангармонического (нелинейного) осциллятора без затухания