Модель "хищник-жертва"

Модель взаимодействия "хищник-жертва" независимо предложили в 1925-1927 гг. Лотка и Вольтерра. Два дифференциальных уравнения (листинг 11.7) моделируют временную динамику численности двух биологических популяций жертвы y₀ и хищника y₁. Предполагается, что жертвы размножаются с постоянной скоростью C, а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи (с коэффициентом r) и умирают естественным образом (смертность определяется константой D). 

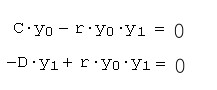
Модель замечательна тем, что в такой системе наблюдаются циклическое увеличение и уменьшение численности и хищника (рис.1), и жертвы, так часто наблюдаемое в природе. Фазовый портрет системы представляет собой концентрические замкнутые кривые, окружающие одну стационарную точку, называемую центром. Как видно, модельные колебания численности обеих популяций существенно зависят от начальных условий - после каждого периода колебаний система возвращается в ту же точку. Динамические системы с таким поведением называют негрубыми.

Решения:

 Фазовый портрет: