ОДУ > Задачи Коши > Алгоритм Розенброка   

С самого начала исследования жестких ОДУ было замечено, что они лучше поддаются решению неявными методами. В частности, можно применять различные неявные вариации многошаговых алгоритмов. Ради примера приведем одну из неявных схем Адамса: 

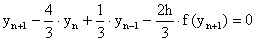
Вообще говоря, в случае жестких ОДУ требования к численному методу заключаются в [см. Федоренко]:
1. согласованности (схема должна аппроксимировать ОДУ);
2. соответствии специальным требованиям устойчивости;
3. необходимости пройти ряд вычислительных тестовых задач. 

Для реализации приведенной схемы Адамса (или любой другой неявной схемы) на каждом шаге по времени придется решать приведенную систему нелинейных алгебраических уравнений. В последнее время появились алгоритмы, в которых система нелинейных уравнений не решается. Приведем основные идеи довольно популярного алгоритма Розенброка, реализованного в ряде математических пакетов, в частности, MathCAD 200X.

Алгоритм Розенброка решения системы жестких уравнений 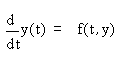(y и f - векторы) основан на следующих действиях, выполняемых на каждом шаге:
1. Вычисляется матрица производных в точке y_n: A=f_y(y_n). 
2. Следующая точка y_n+1 находится из матричного уравнения:
,
 в котором постоянные параметры алгоритма имеют, к примеру, такие значения:

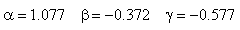
 Таким образом, алгоритм Розенброка является одношаговым и явным (не требуется решения нелинейных уравнений на каждом шаге). Однако, как видно из формулы алгоритма, пересчет каждого шага требует:
 во-первых,  численного определения производных функции f_y (не забывайте, что в случае системы ОДУ y(t) - это вектор);
и во-вторых, решения системы линейных уравнений (поскольку искомые компоненты вектора y_n+1 входят в матричное уравнение в линейной комбинации).

Алгоритм Розенброкка, благодаря своей вычислительной простоте, реализован во многих математических пакетах для ЭВМ, в частности, в MathCAD.