Постановка задачи для уравнения теплопроводности
Дифференциальное уравнение теплопроводности (или,
по-другому, диффузии тепла) записывается
следующим образом:
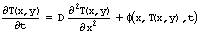
Это уравнение параболического типа, содержащее первую производную по времени t и вторую по пространственной координате x. Оно описывает динамику температуры T(x,t) например, остывающего или нагреваемого металлического стержня (функция T описывает профиль температуры по координате х вдоль стержня).
Коэффициент D называется коэффициентом теплопроводности (диффузии). Он может быть как постоянным, так и зависеть, как явно от координат, так и от самой искомой функции D(x,T,t). Если данная зависимость является нелинейной, то нелинейным становится и само уравнение, что приводит к характерным его решениям.
Функция f(x,T(x,t) ,t) описывает распределение источников тепла вдоль стержня, а также их зависимость от температуры. Опять-таки, если f зависит от T(x,t) нелинейно, нелинейным становится и само уравнение.
Примеры решения нелинейных уравнений теплопроводности приведены здесь.
Линейное уравнение теплопроводности имеет аналитическое решение, а пример его численного решения Вы найдете на следующей странице.