Нелинейная динамика
и теория самоорганизации
Исследование задач теории горения и взрыва, физики плазмы, открытие в ходе вычислительного эксперимента эффекта Т-слоя привлекло внимание учёных к анализу неустойчивостей в сплошных средах. Ряд таких неустойчивостей развивается в режиме с обострением, когда некоторые переменные, характеризующие объект, неограниченно растут за ограниченное время.
В Институте были выполнены пионерские работы по теории режимов с обострением. В ходе этих работ было обнаружено парадоксальное явление - эффект локализации тепла [133], исследованы пространственно-локализованные структуры и выяснены законы их организации, созданы новые математические методы (метод операторного сравнения, метод приближенных автомодельных решений и др.). Эти теоретические исследования получили мировое признание; они нашли приложение в задачах лазерной термохимии, СВЧ-пробоя, химической кинетики, физики плазмы [134].
Одним из фундаментальных результатов прикладной математики стало открытие динамического хаоса - непериодического, неупорядоченного поведения, описываемого детерминированными системами, в которых траектория однозначно определяется начальными данными [135]. Использование этого явления позволяет создавать новые методы диагностики, защиты и обработки информации, системы мониторинга и прогноза. В Институте были построены алгоритмы, позволяющие анализировать количественные характеристики хаоса, упрощенные модели, помогающие понять это явление, предложены новые типы прогнозирующих систем [136], нейронные сети, где элементы могут вести себя хаотическим образом [137]. Развитые подходы эффективно использовались в теории солнечного и земного динамо, задачах гидродинамики и медицинской диагностики.
Важный класс нелинейных процессов в сплошных средах связан с хаотическими, турбулентными режимами. В Институте был выполнен большой цикл исследований, посвященный таким режимам в системах реакция-диффузия - диффузионному хаосу. Основным результатом этих работ стало построение иерархии упрощенных моделей для таких систем. Эта иерархия включает в себя ряд модельных уравнений в частных производных, обыкновенных дифференциальных уравнений, одномерных и двумерных отображений. Их анализ позволил выяснить сценарии возникновения хаоса в большом классе систем типа реакция-диффузия, а также обнаружить ряд важных качественных эффектов [138].
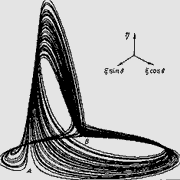
Математическим образом динамического хаоса являются странные аттракторы. На рис. 28 показан странный аттрактор системы трех обыкновенных дифференциальных уравнений, входящей в построенную иерархию. Геометрическая теория, развитая для таких объектов, позволяет выяснить механизм возникновения динамического хаоса [139].
Работы в этом направлении вносят важный вклад в теорию самоорганизации, синергетику - междисциплинарный подход, активно развивающийся в мире и в России. В рамках этого подхода предложен и ряд высоких технологий, и новые пути решения фундаментальных научных проблем, и новые стратегии [140,141,142].