|
Николай Николаевич Ченцов
некрологи, соболезнования
Некролог
(Успехи математических наук)
УСПЕХИ МАТЕМАТИЧЕСКИХ НАУК
1993. Т. 48, вып. 2
(290). С. 165-168

5 июля после
тяжелой болезни скончался доктор физико-математических наук Николай
Николаевич Ченцов -
заведующий отделом Института прикладной математики им. М.В. Келдыша
Российской академии наук.
Николай
Николаевич родился 19 февраля 1930 г. в г. Москве. Отец - Николай
Гаврилович Ченцов (1882-1968) окончил математическое отделение
физико–математического факультета Московского университета в 1904 г.,
работал научным сотрудником ЦАГИ (с момента основания в 1918 г. до
выхода на пенсию в 1958 г.). Ученик и сотрудник Н.Е. Жуковского,
занимался теорией упругости, теорией композитов, газовой динамикой и др.
Мать – Екатерина Ивановна Ченцова (урожденная Дорофеева) (1891-1960) окончила
5 курсов медицинского отделения Московских Высших женских курсов, до
рождения сына работала фельдшером.
Интерес к
математике у Коли Ченцова проявился достаточно рано. Восьмиклассником он
пришел в школьный математический кружок для IX-X классов при механико–математическом
факультете МГУ, которым руководили аспирант А.С. Кронрод и студентка
О.А. Ладыженская, и получил II премию по VIII
классам на Московской Математической Олимпиаде. В X классе он занимался в кружке
для IX–X
классов под руководством аспиранта Е.Б. Дынкина, на X
олимпиаде получил I премию.
В
1947 г. Н.Н. Ченцов поступил на механико–математический факультет
МГУ и очень активно включился в руководство школьным кружком и проведение
олимпиад. Он был ответственным секретарем XIV Московской
Математической Олимпиады и секретарем Совета по олимпиадам при Ректорате
МГУ (одновременно с Р.В. Хохловым). Студент Коля Ченцов был одним из
авторов трехтомника «Избранные задачи и теоремы элементарной математики».
Особенно много труда вложил он в написание III тома
«Стереометрия».
Научная
работа Н.Н. Ченцова началась на семинаре Е.Б. Дынкина, под его
руководством он пишет дипломную работу «Асимптотическая теория
статистических оценок».
В
1952 г. он с отличием окончил мех.–мат. и получил официальную
рекомендацию в аспирантуру МГУ, но по распоряжению И.Г. Петровского
был направлен в Расчетное бюро МИАН им. В.А. Стеклова. Там в то время
были сосредоточены вычислительные работы в обеспечение решения атомной
проблемы. Руководил этими работами М.В. Келдыш. По просьбе
И.Г. Петровского Н.Н. Ченцову, в порядке исключения, было
разрешено сочетать работу с учебой в заочной аспирантуре МИАН, где он
продолжил занятия статистикой у Н.В. Смирнова.
В Расчетном
бюро Н.Н. Ченцов был определен сначала инженером, а потом младшим
научным сотрудником в группу И.М. Гельфанда. Основным содержанием его
деятельности в 1952-1959 гг.
стали разработки алгоритмов и проведение расчетов в задачах переноса и
рассеяния излучения в сложных системах. Эти расчеты проводились по заданиям
Я.Б. Зельдовича, А.Д. Сахарова и их сотрудников. За их выполнение
Н.Н. Ченцов в 1956 г. был награжден Орденом Трудового Красного
Знамени. Последующие результаты этого цикла работ были отмечены
присуждением Н.Н. Ченцову в составе авторского коллектива Государственной
премии (1972 г.).
Одновременно
с этими работами Н.Н. Ченцов совместно с М.В. Келдышем,
К.И. Бабенко, Н.А. Дмитриевым и другими сотрудниками уже
Отделения прикладной математики МИАН (в которое в 1953 г. объединением
с группой А.Н. Тихонова было преобразовано Расчетное бюро) участвовал
в пионерской работе по расчету нестационарного газодинамического течения,
порождаемого движением осесимметрической ударной волны. В этой работе были
разработаны и реализованы оригинальный способ математического описания
двумерного течения и вычислительный алгоритм решения подобных задач - «матричная
прогонка».
Научный
интерес к проблеме кумуляции сохранился у Н.Н. Ченцова на протяжении
всех лет его работы. Вместе с Ю.Н. Бабаевым и другими соавторами были
разработаны оригинальные газодинамические конструкции, реализующие
сферическую кумуляцию, и построены приближенные методы, позволяющие
проводить предварительный отбор решений, близких к оптимальному, по отбору
кумулирующей энергии. Эти исследования являют собой красивое и эффективное
сочетание аналитических построений с результатами численных расчетов
двумерных нестационарных течений со сложной геометрией.
Одновременно
в эти годы Н.Н. Ченцов выполнил в семинаре Е.Б. Дынкина работу
«Слабая сходимость случайных процессов с траекториями без разрывов второго
рода и так называемый «эвристический» подход к критериям согласия типа
Колмогорова-Смирнова»
(«Теория вероятностей и её применения, Т. 1, в. 1, 1956), где он
дал простой критерий:
(1) p,
q
> 0, M|xn(t
- t) - xn(t)|p × |xn(t)
- xn(t+q)|q £ c(t + q)1+e,
чтобы
траектория сепарабельного процесса xn(t)
с вероятностью единица не имела разрывов второго рода (получивший затем
название критерия Колмогорова-Ченцова,
так как он обобщает критерий Колмогорова непрерывности почти наверное
сепарабельного процесса)
p
> 0, M|x(t + t) - x(t)|p < |t|1+e.
Ченцов также
показал, что если для процессов xn(t)
неравенство (1) выполнено с одними и теми же константами p,
q и e > 0
на одном и том же отрезке T
оси t,
то при слабой сходимости конечномерных распределений xn(t)
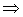 x0(t)
вероятность попадания в полосу также сходится x0(t)
вероятность попадания в полосу также сходится
Pn{a £ xn(t)
£ b,"t Î T} 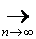 P0{a
£ x0(t) £ b,"t Î T}, P0{a
£ x0(t) £ b,"t Î T},
что дает
простейшее, по мнению Биллингслея, обоснование эвристического принципа Дуба
вычисления асимптотических критериев типа Колмогорова-Смирнова
предельным переходом от центральной эмпирической функции распределения к
броуновскому мосту. Эти результаты легли в основу кандидатской диссертации
Н.Н. Ченцова «Обоснование статистических критериев методами случайных
процессов», защищенной в 1958 г.
Работа
«Многопараметрическое броуновское движение Леви и обобщенный белый шум»
(«Теория вероятностей и ее применения», Т. 2, в. 2, 1957),
посвящена конструкции методами интегральной геометрии случайных полей Леви z(t)
-
аналогов винеровского процесса, у которого время заменено многомерным
параметром, пробегающим или все n - мерное
пространство или n - мерную
сферу. Конструкция, связывающая поля Леви с белым шумом на грассманианах, доказывала
существование таких полей и сильно упрощала их теорию. Эти две работы
принесли Н.Н. Ченцову широкую известность. Следует отметить еще
многомерное обобщение броуновского движения -
случайное поле Китагавы-Ченцова
z(x,y)
и аналог моста для него -
возникающей при изучении предельных распределений Fn(x,y)
многомерной случайной величины (x,h)
с независимыми координатами x и h.
Он установил непрерывность этого поля и показал применимость принципа Дуба
для вычисления предельного распределения функционалов от таких многомерных
функций.
Исследования
сепарабельных процессов без разрывов второго рода заставили
Н.Н. Ченцова изучить теорию меры в тихоновских степенях 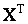 , где он дал (1958 г.) первые примеры неборелевских
подмножеств пространства , где он дал (1958 г.) первые примеры неборелевских
подмножеств пространства 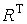 , где T -
отрезок вещественной прямой. Эти результаты были изложены в статье
«Неизмеримые подмножества Тихоновского куба» в сборнике, посвященном
А.Н. Тихонову. , где T -
отрезок вещественной прямой. Эти результаты были изложены в статье
«Неизмеримые подмножества Тихоновского куба» в сборнике, посвященном
А.Н. Тихонову.
Практическим
выводом его теоретических исследований по теории вероятностей и
математической статистике явился большой вклад в развитие и применение
методов моделирования, отмеченный в 1979 г. Государственной премией
СССР (в коллективе авторов). Его работы в этой области можно условно
разбить на три направления:
1. Принципы
метода Монте-Карло,
способы ускорения вычислений и обработок результатов (совместно со своим
сотрудником А.С. Фроловым).
2. Задачи
теории переноса -
расчет критического параметра реактора на быстрых нейтронах, о
распределении гамма-излучения в воздухе и расчете характеристик нейтронного
спектрометра.
3. Кубатурные
формулы для кратных и бесконечно-кратных
интегралов. Теория численных кубатур бесконечно-кратных
интегралов ведет начало с расчетов И.М. Гельфанда и Н.Н. Ченцова
«О численном вычислении континуальных интегралов» (ЖЭТФ. Т. 31,
в. 6 (12), 1956) и исследований Н.Н. Ченцова «О квадратурных
формулах для функций бесконечно большого числа переменных» (ЖВМ и МФ.
Т. 1, № 3, 1961).
Большое
значение в становлении советской школы статистического моделирования имели
лекции Н.Н. Ченцова по основам и принципам метода Монте-Карло,
прочитанные в 1958-1959,
1959-1960
учебных годах в МГУ, а также в ряде школ тех лет по вычислительной
математике.
Вместе с
Н.М. Коробовым и Н.С. Бахваловым Н.Н. Ченцов руководил семинаром
в отделе Теории чисел МИАН, где рассматривались вопросы вычисления
интегралов высокой размерности и конструирования псевдослучайных чисел.
Занимаясь в
60-е годы проблемой наиболее точного определения плотности случайной
величины по наблюдениям, Н.Н. Ченцов пришел к идее поиска естественной
геометрии семейств вероятностных законов. Различные геометрические аспекты
математической статистики обсуждались тогда А.Н. Колмогоровым,
С.Р. Рао, С. Кульбаком и другими исследователями. Итогом
изысканий Н.Н. Ченцова явилось создание в 1964 г. красивой
своеобразной геометрии статистических решений с категорией марковских
отображений (обобщающей группу движений в обычной геометрии). В терминах
этой фундаментальной категории естественно описываются наиболее существенные,
глубинные свойства объектов теории статистических решений А. Вальда,
Д. Блекуэлла, Ч. Стейна, получает прозрачное объяснение
исключительная роль фишеровского информационного тензора, как порождающего
единственную монотонно инвариантную метрику в этой категории, и
экспоненциальных семейств, как геодезических относительно некоторой
инвариантной аффинной связности. Н.Н. Ченцовым было открыто целое
семейство таких связностей, получивших впоследствии название связностей
Ченцова-Амари.
Н.Н. Ченцов
рассмотрел единую модель ряда классических задач математической статистики
как обратных задач теории вероятностей и нашел изящные и емкие формулировки
асимптотических границ рисков в терминах размерности параметра, либо
поперечников Колмогорова и внутренних радиусов Никольского априорных
бесконечномерных семейств. Им установлена некорректность задачи оценки
неизвестного распределения при отсутствии априорной информации.
Эти
исследования подытожены в докторской диссертации «Общая теория
статистического вывода» (1968 г.) и в монографии «Статистические
решающие правила и оптимальные выводы» («Наука», 1972). Однако, высказанные
в ней идеи, по-видимому, казались в те годы необычными и не получили
широкого распространения. Сыграл роль и научный стиль математического творчества
Н.Н. Ченцова, адресованного посвященным и чуждого какой-либо
саморекламе. Впоследствии геометрический подход систематически развивался в
работах ряда зарубежных ученых и в настоящее время является одним из важных
современных направлений в математической статистике. Благодаря переводу
монографии на английский язык (Американское математическое общество,
1982 г.) все более широкое международное признание получает и
основополагающий вклад Н.Н. Ченцова.
В 70-е годы
Н.Н. Ченцов, совместно с Е.А. Морозовой, начинает работать в
новой, быстро развивающейся области -
некоммутативной теории вероятностей, перенося свой категорно-геометрический
подход на квантовую статистику. Была выяснена неполнота системы операций
квантовой логики Биркгофа - фон Неймана и указана полная система, построена
эргодическая теория для квантовых цепей Маркова. Одним из последних
значительных достижений явилось описание целого класса инвариантных
монотонных римановых метрик в пространстве квантовых состояний.
Тот факт, что
уже в свои зрелые годы Н.Н. Ченцов сумел творчески освоить и
плодотворно работать в такой новой и трудной для вероятностника,
воспитанного в классических традициях теории множеств, области, лишний раз
свидетельствует о силе и свежести его математического дарования, столь
безвременно утраченного для нас.
Всю свою
жизнь Н.Н. Ченцов оставался однолюбом и по отношению к выбранной
научной стезе, к товарищам по работе и к дорогому ему Институту прикладной
математики им. М.В. Келдыша, где проработал без малого сорок лет. На
протяжении многих лет он был ученым секретарем Института, являя образец
неформального исполнения этой должности. Таким же он был и заведующим
отделом.
Очень многое
сделано Н.Н. Ченцовым по увековечению памяти М.В. Келдыша.
Организация Кабинета-музея, общественным директором которого он был
назначен, подготовка и издание «Избранных трудов» М.В. Келдыша,
написание большого числа статей о выдающемся ученом для научных и
общественных изданий, участие в создании двух документальных фильмов - вот далеко
не полный перечень сделанного Н.Н. Ченцовым в память о почитаемом им
Директоре.
Научная
широта, глубокая эрудиция, энциклопедичность знаний, беззаветная
преданность науке, необыкновенное трудолюбие, принципиальность,
порядочность. Таким человеком и ученым навсегда останется Николай
Николаевич Ченцов в памяти тех, кто хорошо его знал.
В.И. Арнольд,
Н.С. Бахвалов, К.В. Брушлинский, И.М. Гельфанд,
Р.Л. Добрушин,
А.В. Забродин, И.А. Ибрагимов, С.П. Курдюмов,
С.П. Новиков,
Д.Е. Охоцимский, Ю.В. Прохоров, Ю.Б. Радвогин
Я.Г. Синай, Р.З. Хасьминский, А.С. Холево,
А.Н. Ширяев, Т.М. Энеев
Некролог
(Теория вероятностей и ее применения)
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ И ЕЕ ПРИМЕНЕНИЯ
1993.
Т. 38, вып. 3 с. 613-623
Николай Николаевич Ченцов
(19.II.1930
-
05.VII.1992)
5 июля 1992
года после тяжелой болезни скончался Николай Николаевич Ченцов - выдающийся
ученый в области чистой и прикладной математики, работавший в разнообразных
областях теории вероятностей, математической статистики, теории случайных
процессов, теории меры, функциональном анализе, теории численных методов и
ее приложениях.
Н.Н. Ченцов
родился 19 февраля 1930 г. в Москве в
семье научного работника. Его отец -
Николай Гаврилович Ченцов, ученик и соратник профессора
Н.Е. Жуковского, -
был известным "упругистом", проработавшим с 1918 г.
по 1958 г.
в ЦАГИ. Большую известность получила его работа «Исследование фанеры как
ортотропной пластинки».
Фамильный
интерес к математике у Николая Николаевича проявился довольно рано. Когда
осенью 1944 г.
при механико–математическом факультете МГУ после реэвакуации снова стал
работать математический кружок, восьмиклассник Коля Ченцов начинает посещать
секцию общего типа 8-9 классов, в руководстве которого участвовали
А.С. Кронрод, О.А. Ладыженская.
В 1946 г.
он переходит в секцию Е.Б. Дынкина, позднее превратившуюся сначала в
семинар для студентов младших курсов, а потом в «большой семинар
Е.Б. Дынкина», в котором проходило становление таких математиков, как
Р.Л. Добрушин, А.А. Юшкевич, Ф.И. Карпелевич,
Р.З. Хасьминский, В.М. Золотарев, А.Д. Вентцель и др.
Поступив в
1947 г.
на механико-математический
факультет МГУ, Н.Н. Ченцов начинает принимать активное участие в
работе со школьниками -
руководит секциями геометрии и прикладной математики с С.К. Годуновым
и секцией общего типа с Е.А. Морозовой. В 1949 г.
А.С. Кронрод уговаривает Ченцова принять участие в работе над
«Избранными задачами и теоремами элементарной математики». Особенно много
труда Николай Николаевич вложил в написание книги «Стереометрия» и
подготовку чертежей для нее.
В 1952 г.
Н.Н. Ченцов заканчивает Московский университет, защитив дипломную
работу «Асимптотическая теория статистических оценок» (руководитель -
Е.Б. Дынкин), посвященную фундаментальному вопросу математической
статистики о существовании эффективных оценок и давшую приемлемое
обоснование асимптотической оптимальности оценок максимального
правдоподобия. (Эти результаты были опубликованы в Трудах 3-го Всесоюзного
математического съезда, Москва, июнь-июль
1956 г.)
По окончании
университета Н.Н. Ченцов был направлен на работу в Расчетное бюро
Математического института им. В.А. Стеклова Академии наук СССР (МИАН)
и в порядке исключения ему разрешили (по просьбе И.Г. Петровского)
поступить в безотрывную аспирантуру института, где он продолжил занятия
математической статистикой у Н.В. Смирнова. Основным же содержанием
его научной деятельности в 1952-1959 гг.
стала работа по заданиям Я.Б. Зельдовича и А.Д. Сахарова и их
сотрудников, состоящая в разработке алгоритмов и проведении расчетов в
задачах переноса и рассеяния излучения в сложных системах атомной
энергетики.
В связи с
этими и другими задачами возникла настоятельная необходимость практического
вычисления интегралов очень высокой размерности. Классические методы
решения подобных задач оказывались мало пригодными, и в тот период
Н.Н. Ченцов вел активную пропаганду необходимости принципиально новых
подходов к решению таких задач и сам занимался разработкой нетрадиционных
методов и их практической реализацией. Именно в это время совместно с
И.М. Гельфандом он реализовал в ряде задач переноса сведение
вычисления континуальных интегралов к интегралам конечной размерности (большей
трехсот) с последующим применением вероятностных методов. (Соответствующие
результаты были доложены на 2-й Женевской конференции по мирному
использованию атомной энергии [1]).
Центральным
местом в проблематике рассеяния занимает задача определения плотности p
= p(x)
нейтронов или плотности p
= p(x)
рождения нейтронов, которую надо путем обработки извлечь из имитаций
историй движения нейтронов. Ранее для этого применяли классический метод
гистограмм, точность которого невелика и который требует довольно большого
объема памяти для достаточно точной регистрации фактов «деления».
Н.Н. Ченцов предложил новый подход для вычисления плотности p
= p(x),
основываясь на замечании, что
коэффициент разложения плотности p(x)
случайной величины x
по системе ортонормированных с весом r(x)
функций j0(x),…, jn(x)
имеет вид
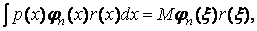
где
математическое ожидание берется по всем точкам деления на случайной
траектории.
Эта идея
впоследствии не раз переоткрывалась, но приоритет Н.Н. Ченцова был
признан и его проекционные оценки нашли место в арсенале методов оценки
плотности неизвестного распределения случайной величины по ее наблюдениям.
В 1958-1960 гг.
Николай Николаевич по предложению А.Н. Колмогорова читает на мех-мате
МГУ курсы лекций по теории метода Монте-Карло,
повторяя их затем для сотрудников Всесоюзного института экспериментальной
физики. Эти лекции сыграли заметную роль в широком распространении этих
методов в нашей стране.
В эти же годы
вместе с Н.С. Бахваловым и Н.М. Коробовым Николай Николаевич
руководит в отделе теории чисел МИАН семинаром «Трех Коль», в котором
исследовались вопросы вычисления интегралов высокой размерности, изучались
вопросы о том, какие свойства стохастических квадратурных формул можно
перенести в классическую теорию кубатурных формул.
Занимаясь в
шестидесятые годы проблемой наиболее точного определения плотности p
= p(x) случайной величины x по
наблюдениям, Н.Н. Ченцов пришел к идее поиска естественной геометрии
семейств вероятностных законов. Различные геометрические аспекты математической
статистики обсуждались тогда А.Н. Колмогоровым (например, в его
лекциях в институте А. Пуанкаре в 1955 г.), С.Р. Рао,
С. Кульбаком и др. Предлагались разного рода метрики, в том числе
риманова метрика с матрицей информации Фишера, задающей метрический тензор.
При этом, однако, «красивых» формул не получилось.
Николай
Николаевич попробовал искать естественную аффинную (линейную) связь.
Результатом явилась работа «Геометрия «многообразия» распределения
вероятностей» [2], в которой, в частности, была рассмотрена так называемая
плоская связность. При этом геодезическими линиями и вполне геодезическими
многообразиями в ней были хорошо известные экспоненциальные семейства с
канонической параметризацией.
Следующим
шагом Н.Н. Ченцова явилось создание красивой и своеобразной геометрии
статистических решений с категорией марковских отображений, в терминах
которой нашли свое естественное описание существенные свойства объектов
теории статистических экспериментов и решений (введенных и рассмотренных А. Вальдом,
Д. Блекуэллом, Ч. Стейном и др.).
В рамках
своего подхода Н.Н. Ченцов получает прозрачное объяснение
исключительности фишеровского информационного тензора, как порождающего
единственную монотонно инвариантную метрику в этой категории и роль
экспоненциальных семейств, как геодезических относительно некоторой
инвариантной аффинной связности. Им было также открыто целое семейство
таких связностей, получивших впоследствии название «связностей Ченцова-Амари».
Н.Н. Ченцов
рассмотрел единую модель ряда классических задач математической статистики
как обратных задач теории вероятностей и нашел изящные и емкие формулировки
асимптотических границ рисков либо в терминах размерности параметра, либо
поперечников Колмогорова и внутренних радиусов Никольского и априорных
бесконечномерных семейств.
Эти
исследования были подытожены в монографии «Статистические решающие правила
и оптимальные выводы» в 1972 г. [3]. Высказанные в этой монографии
идеи, по-видимому, казались в те годы необычными и даже далекими от
собственно статистических проблем. Однако сейчас геометрический подход
является одним из важных современных направлений в математической
статистике, и основополагающий вклад Н.Н. Ченцова получил широкое
международное признание.
В семидесятые
годы Н.Н. Ченцов совместно с Е.А. Морозовой начинает работать в
новой, быстро развивающейся области -
некоммутативной теории вероятностей, перенося категорно-геометрический
подход на квантовую статистику. Ими была выяснена неполнота системы
операций квантовой логики Биркгофа-фон
Неймана и указана полная система [4], построена эргодическая теория
квантовых цепей Маркова. Одним из последних значительных достижений явилось
описание целого класса инвариантных монотонных римановых метрик в
пространстве квантовых состояний.
В первом
выпуске первого тома нашего журнала «Теория вероятностей и ее применения»
за 1956 г. была опубликована ставшая теперь широко известной работа
Н.Н. Ченцова «Слабая сходимость случайных процессов с траекториями без
разрывов второго рода и так называемый «эвристический» подход к критериям
согласия типа Колмогорова -
Смирнова» [5].
Известно, что
значительный интерес к предельным теоремам для случайных процессов был
вызван необходимостью обосновать вывод распределения для критерия согласия
Колмогорова. Другим важным стимулом были предельные теоремы для
функционалов от сумм независимых случайных величин, которые явились в
какой-то мере обобщениями центральной предельной теоремы
(А.Н. Колмогоров, А.Я. Хинчин).
Весьма
существенным продвижением в теории предельных теорем для случайных
процессов был известный «принцип инвариантности» М. Донскера
(1951 г.) и его обобщения Ю.В. Прохорова (1956 г.). Тем
самым принципиальные вопросы теории предельных теорем для непрерывных
процессов были выяснены.
Однако
приходится рассматривать (как, скажем, в случае эмпирических функций
распределений) и предельные теоремы для разрывных процессов. Именно к тому
кругу вопросов и относится рассматриваемая работа Н.Н. Ченцова,
стремившегося найти такую предельную теорему, которая бы охватывала случай
сходимости эмпирических функций распределения.
На этом пути
им было прежде всего получено следующее обобщение известного критерия
Колмогорова (о существовании непрерывной модификации у случайного процесса)
на случай разрывных процессов: если
X
= (Xt), t Î [0,1],
-
сепарабельный случайный процесс
такой, что для некоторых a ³ 0, b ³ 0, C > 0
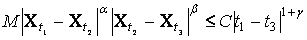
для 0 £ t1 < t2 < t3 £ 1, то с
вероятностью единица процесс имеет траектории без разрывов второго рода.
Опираясь на
этот критерий, получивший впоследствии название «критерий Колмогорова-Ченцова»,
Николай Николаевич доказывает следующий результат: если последовательность сепарабельных случайных процессов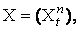 0 £ t
< 1, n ³ 1, такова, что их конечномерные распределения
слабо сходятся к конечным распределениям сепарабельного процесса
X
= (Xt), 0 £ t
< 1, и при некоторыхa ³ 0, b ³ 0, C > 0 (не
зависящих от n) 0 £ t
< 1, n ³ 1, такова, что их конечномерные распределения
слабо сходятся к конечным распределениям сепарабельного процесса
X
= (Xt), 0 £ t
< 1, и при некоторыхa ³ 0, b ³ 0, C > 0 (не
зависящих от n)
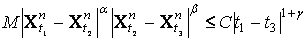
для 0 £ t
< t2 < t3 £ 1, то для
любых двух непрерывных функций f = f(t)
и g
= g(t)
с f(t)
< g(t),
t Î [0,1],
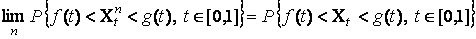 . .
Этот
результат дал простейшее обоснование «эвристического» принципа Дуба
вычисления асимптотических критериев типа Колмогорова - Смирнова
предельным переходом от центрированной эмпирической функции к броуновскому
мосту.
Сформулированные
результаты Н.Н. Ченцова, послужившие основой его кандидатской
диссертации «Обоснование статистических критериев методами случайных
процессов» (1958 г.), стимулировали многие последующие исследования.
Широкую
известность получила выполненная Н.Н. Ченцовым в тот же период работа
«Многопараметрическое броуновское движение Леви и обобщенный белый
шум» [6], посвященная конструкции (методами интегральной геометрии)
случайных полей Леви -
аналогов винеровского процесса, у которых время заменено многомерным
параметром, пробегающим или все n - мерное
пространство или n -
мерную сферу. Данная Ченцовым конструкция, связывающая поле Леви с белым
шумом на грассманианах, доказывала существование таких полей и сильно
упрощала их теорию.
В этот же
период Н.Н. Ченцов рассмотрел еще одно многомерное «обобщение
броуновского движения -
случайное поле Китагавы -
Ченцова» и аналог броуновского моста для него, возникающих в качестве
предельных распределений для эмпирической функции распределения многомерного случайного вектора.
Им была
установлена непрерывность введенного случайного поля, построено
соответствующее обобщение «критерия Колмогорова - Ченцова» и
показана применимость «эвристического» принципа Дуба для вычисления
предельного распределения функционалов от таких многомерных функций.
Исследование
сепарабельных случайных процессов без разрывов второго рода привело
Н.Н. Ченцова также к изучению структуры множеств в континуальных
пространствах. В частности, им были даны (1958 г.) первые примеры неборелевских
подмножеств пространства 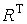 , где T -
отрезок вещественной прямой. , где T -
отрезок вещественной прямой.
Много времени
и сил Н.Н. Ченцов отдавал научно-организационной работе - с
1959 г. по 1966 г. он работал ученым секретарем Отделения
прикладной математики Математического института имени В.А. Стеклова
Академии наук СССР; с 1988 г. -
заведующий отделом Института прикладной математики; в 1979 г. был
назначен директором (на общественных началах) Мемориального кабинета-музея
академика М.В. Келдыша при Президиуме АН СССР; являлся членом Научного
совета по математическому моделированию и Комиссии по функциональному
анализу при Отделении математики Академии наук, членом ряда
специализированных ученых советов; был одним из ответственных редакторов
томов «Математика» и «Механика» избранных трудов М.В. Келдыша.
В
1956 г. за выполнение прикладных работ Николай Николаевич был
награжден Орденом Трудового Красного Знамени, а в 1972 и 1979 годах в
составе авторских коллективов ему присуждалась Государственная премия.
В последние
годы своей жизни Н.Н. Ченцов активно занимался разработкой методов
расчета и проектирования осесимметричных систем с кумуляцией энергии.
Научная
широта, глубокая эрудиция, энциклопедичность знаний, беззаветная
преданность науке, необыкновенное трудолюбие, принципиальность, скромность
и порядочность -
вот те черты и качества, которые слились в образе Николая Николаевича
Ченцова, так рано, безвременно ушедшего из жизни.
Н.С. Бахвалов, А.А. Боровков,
Р.Л. Добрушин, А.В. Забродин,
В.М. Золотарев, И.А. Ибрагимов,
Ю.В. Прохоров, Б.А. Севастьянов,
Я.Г. Синай, А.В. Скороход,
В.А. Статулявичус, Р.З. Хасьминский,
А.С. Холево, Д.М. Чибисов,
А.Н. Ширяев,
СПИСОК
РАБОТ, НА КОТОРЫЕ ЕСТЬ ССЫЛКИ В ТЕКСТЕ.
1. О
применении метода случайных испытаний (метода Монте-Карло) для решения
кинетического уравнения -//
Труды Второй международной конференции ООН по мирному использованию атомной
энергии. ¾
М.: Атомиздат. 1959. ¾
Т. 2. С. 628-633 (совм. с
И.М. Гельфандом, А.С. Фроловым, С.М. Фейнбергом).
2. Геометрия
«многообразия» распределения вероятностей // Докл. АН СССР. 1964. Т. 158, № 3. С. 543-546
3.
Статистические решающие правила и оптимальные выводы. ¾
М.: Наука, 1972. 520 с.
4. Элементы
стохастической квантовой логики. ¾
Новосибирск, 1977. 16 с. ¾
Препринт ИМ СО АН СССР (совм. с
Е.А. Морозовой).
5. Слабая сходимость случайных
процессов с траекториями без разрывов второго рода и так называемый
«эвристический» подход к критериям согласия типа Колмогорова- Смирнова //
Теория вероятностей и ее применения. 1956. Т. 1, вып. 1.
С. 155-161.
6.
Многопараметрическое броуновское движение Леви и обобщенный белый шум //
Теория вероятностей и ее применения. 1957. Т. 2, вып. 2.
С. 281-282.
|