ВЕЙВЛЕТНЫЙ АНАЛИЗ
В последнее время возрос интерес к другим интегральным преобразованиям, в частности вейвлетному (или дискретному волновому) преобразованию. Оно применяется, главным образом, для анализа нестационарных сигналов и для многих задач подобного рода оказывается более эффективным, чем преобразование Фурье. Основным отличием вейвлетного преобразования является разложение данных не по синусоидам (как для преобразования Фурье), а по другим функциям, называемым вейвлетобразующими. Вейвлетобразующие функции, в противоположность бесконечно осциллирующим синусоидам, локализованы в некоторой ограниченной области своего аргумента, а вдали от нее равны нулю или ничтожно малы. Пример такой функции, называемой "мексиканской шляпой", показан на рис.1.
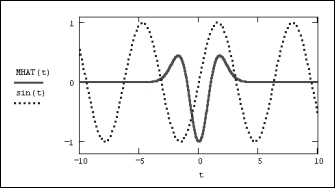
Рис.1. Сравнение синусоиды и вейвлетобразующей функции
Из-за своего математического смысла вейвлет-спектр имеет не один аргумент, а два. Помимо частоты, вторым аргументом b является место локализации вейвлетобразующей функции. Поэтому b имеет ту же размерность, что и x.
Один из примеров расчета вейвлет-спектра
модельной функции приведен ниже:
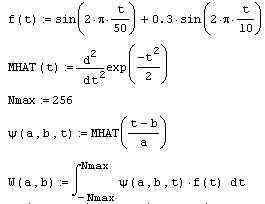
Результат расчетов изображен на рис.2. Анализу, как Вы видите, подвергается функция, составленная из суммы двух синусов, а график двухпараметрического спектра C(a,b) выведен в виде привычных для вейвлет-анализа линий уровня на плоскости (a,b).
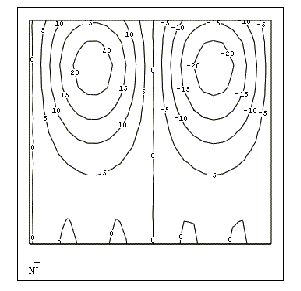
Рис.2. Вейвлет-спектр модельной функции суммы двух синусоид
Дополнительную информацию о вейвлет-анализе можно почерпнуть из Астафьева,1996, а с примером его применения в геофизике ознакомиться на следующей странице.
-
Предыстория появления вейвлетного анализа.
-
Определение вейвлет-спектра.
-
Вейвлет-образующие функции.
-
Зачем нужен вейвлетный анализ.
-
Применение к анализу нестационарных процессов.
-
Примеры вейвлет-спектров некоторых функций (синусоида и т.д.).
-
Применение вейвлетного анализа в геофизике.
-
Многомерный вейвлетный анализ.