Класс динамических систем

Динамическими системами принято называть класс задач, представленных задачами Коши для дифференциальных уравнений (обыкновенных - иначе ОДУ, или в частных производных) или систем таких уравнений. В данной главе мы будем рассматривать исключительно динамические системы (д.с.), описываемые ОДУ, принимая во внимание, что теория д.с. и специфические численные методы наиболее развита для этих, более простых, уравнений.

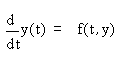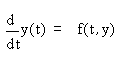Напомним, что задача Коши для системы ОДУ  состоит в отыскании неизвестной векторной функции y(t), включающей несколько (L) неизвестных функций y¹(t), ... , y^L(t), для начального условия y(0)= C. Соответственно числу компонент векторной функции y(t), должно быть поставлено L начальных условий. Исходя из физического смысла такой постановки задачи, можно, не теряя общности, полагать, что дифференциальные уравнения содержат производные по аргументу t, являющемуся временем, и, соответственно, описывают динамику во времени различных физических параметров y(t). Поэтому-то задачи Коши для таких моделей называют динамическими системами, а для их изучения центральным моментом является анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий. 

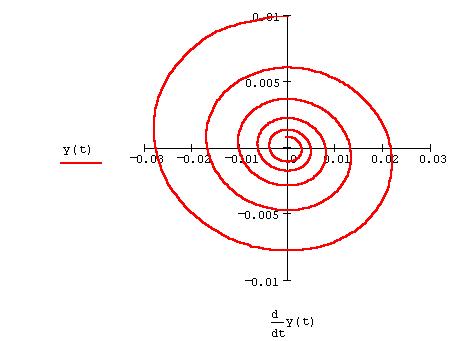
Решения обыкновенных дифференциальных уравнений часто удобнее изображать не в привычном виде y¹(t), ... , y^L(t) (см. рис.1), а в фазовом пространстве, по осям которого откладываются значения каждой из найденных функций. При этом аргумент t входит в графики лишь параметрически (см. рис.2). В случае двух ОДУ такой график – фазовый портрет системы – является кривой на фазовой плоскости и поэтому особенно нагляден. В общем случае, если система состоит из N ОДУ, то фазовое пространство является N-мерным. При N>3 наглядность теряется, и для визуализации фазового портрета приходится строить его различные проекции.

Примечание 

Фазовый портрет типа изображенного на рис.2 имеет одну стационарную точку (аттрактор), на которую "накручивается" решение. В теории динамических систем аттрактор такого типа называется фокусом.

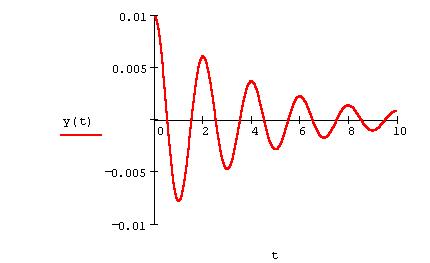
Рис.1 (сверху). Растровый график решения для уравнения затухающего гармонического осциллятора

Рис.2 (снизу). График решения того же уравнения осциллятора в фазовом пространстве