 ОДУ
> Задачи Коши > Свойства
разностных схем
ОДУ
> Задачи Коши > Свойства
разностных схем

Свойства разностных схем Эйлера для ОДУ
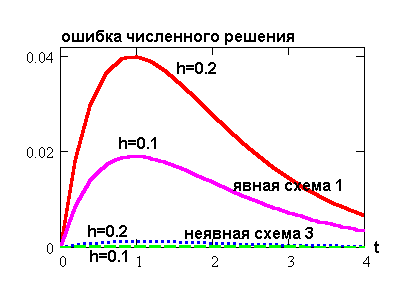
Самое главное свойство - точность. Совершенно естественно, приступая к численному решению дифференциального уравнения, Вы хотите, чтобы полученное Вами решение было как можно ближе к точному решению. Сравним решения нашей линейной задачи с предыдущей страницы, которые предоставляют две из трех приведенных там Эйлеровых схем, с аналитическим решением y(t)=exp(-At). На рисунке сбоку изображена ошибка между аналитическим точным решением и вычисленным с использованием двух шагов. Видно, что неявная схема дает намного меньшие ошибки, чем несимметричная явная. Ошибка падает с уменьшением шага h. В принципе можно оценить (например, с помощью вычислительных тестов) степень уменьшения ошибки в зависимости от величины шага. Окажется, что схема 1 дает решение, которое стремится к точному приh->0 как o(h), а схема 3 - как o(h2). Говорят, что схема обладает N-м порядком ТОЧНОСТИ, если полученное с ее помощью решение стремится к точному решению задачи Коши для ОДУ как o(hN ) при h->0. Схема тем лучше, чем выше порядок точности.
Все сказанное, увы, можно применить к реальности только в модельных случаях, когда и без того известно аналитическое решение задачи Коши. В реальном случае никто точного решения не знает, поэтому порядок точности оценить сложно.
Однако, можно определить порядок аппроксимации уравнения разностной схемой. Естественное требование к схемам - это СОГЛАСОВАННОСТЬ, т.е. переход в пределеh->0 разностной схемы в то самое дифференциальное уравнение, которое решается. Чем меньше шаг h , тем меньше невязка между ОДУ и аппроксимирующим его разностным уравнением. Так вот, N-й порядок АППРОКСИМАЦИИ означает, что невязка стремится к нулю как o(hN ) при h->0. Как аналитически оценивают порядок аппроксимации, сказано в любой книге из приведенных в списке литературы по ОДУ. Если провести несложные выкладки (связанные с разложением в ряд функции y(t) в точке ti ), то легко получить, что схема 1 имеет первый порядок аппроксимации, а схема 3 - второй. В связи с этим и точность этих схем имеет тот же порядок (см. верхний рисунок и обсуждения выше).
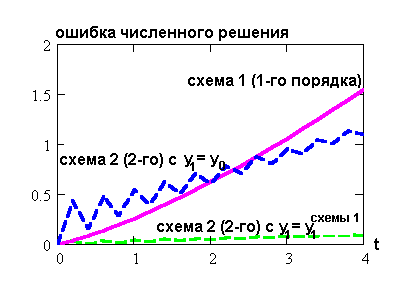
Но не всегда порядок точности совпадает с порядком аппроксимации. Сначала
вспомним о начальных условиях и для этого рассмотрим другой пример. А именно
решение другого ОДУ с правой частью ![]() и н.у. y0. Точное решение задается функцией y(t)=(t+(y0)1/2
)2. Если его искать по схеме 2 (с
поправкой, конечно, на другую правую часть, т.к. у нас уже другая задача),
которая имеет второй порядок аппроксимации, то потребуется на первом
шаге как-то задать y1. Результат расчетов при (самом простом)
выборе y1 = y0 показан синей кривой на рисунке
сбоку. Увы! точность схемы 2 не лучше точности
схемы 1, которая обеспечивает только 1-й порядок
аппроксимации. Так что не все зависит от порядка аппроксимации схемы, важна
еще и соответствующая аппроксимация начальных условий. На том же рисунке
показан расчет по схеме 2, в которой первый шаг делается по формуле схемы1.
Можно еще его улучшить, составив для первого шага аппроксимацию 2-го порядка.
Все сказанное относится и к аппроксимации дифференциальных уравнений и
начальных условий для уравнений в частных производных.
и н.у. y0. Точное решение задается функцией y(t)=(t+(y0)1/2
)2. Если его искать по схеме 2 (с
поправкой, конечно, на другую правую часть, т.к. у нас уже другая задача),
которая имеет второй порядок аппроксимации, то потребуется на первом
шаге как-то задать y1. Результат расчетов при (самом простом)
выборе y1 = y0 показан синей кривой на рисунке
сбоку. Увы! точность схемы 2 не лучше точности
схемы 1, которая обеспечивает только 1-й порядок
аппроксимации. Так что не все зависит от порядка аппроксимации схемы, важна
еще и соответствующая аппроксимация начальных условий. На том же рисунке
показан расчет по схеме 2, в которой первый шаг делается по формуле схемы1.
Можно еще его улучшить, составив для первого шага аппроксимацию 2-го порядка.
Все сказанное относится и к аппроксимации дифференциальных уравнений и
начальных условий для уравнений в частных производных.
Вернемся к решению линейной задачи, сравнив
1-ю и 2-ю схемы. Казалось бы, 2-я схема должна дать лучшее решение, т.к.
обладает лучшим порядком аппроксимации. Но из рисунка сбоку видно, что
решение по схеме 2 не имеет ничего общего с аналитическим
решением. Это происходит потому, что она не обладает важнейшим свойством
- УСТОЙЧИВОСТЬЮ. Устойчивость означает, что погрешности
неточности задания н.у. и вычислительные ошибки, вносимые на каждом шаге
(например, округления) не нарастают чрезмерно (т.е. не забивают в конечном
счете решения). Схема 2 (для рассматриваемой
линейной задачи) абсолютно неустойчива, схема 1
устойчива при h<A/2, а неявная схема 3
устойчива при любом шаге h. В данном случае условия устойчивости можно
определить аналитически, но большинство нелинейных задач исследовать на
устойчивость очень сложно. Поэтому часто для выбора схемы применяют различные
тесты, особенно пристально выискивая подозрительные решения в виде "разболтки".
Как правило, неявные схемы чаще бывают устойчивыми, поэтому для множества
приложений используют именно их, а не простые явные схемы.