Уравнения в частных производных > Введение

Об уравнениях в частных производных 

Дифференциальные уравнения в частных производных требуют нахождения функции не одной, как для ОДУ, а нескольких переменных, например f(x,y). Эти уравнения включают в себя производные по различным переменным (частные производные), например производные по x и по y. Уравнениями в частных производных описывается множество разнообразных физических явлений, и с их помощью можно с успехом моделировать самые сложные явления и процессы (диффузия, гидродинамика, квантовая механика, экология и т. д.). 

В качестве примера дифференциального уравнения в частных производных приведем уравнение теплопроводности (или диффузии тепла):
 

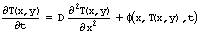
Это уравнение параболического типа, содержащее первую производную по времени t и вторую по пространственной координате x. Оно описывает динамику температуры T(x,t) в присутствии источников тепла f(x,T,t), например, при нагреве металлического стержня. Таким образом, неизвестной функцией, подлежащей определению, является функция T(x,t). Отметим, что данное уравнение линейно, если источник либо не зависит от температуры, либо завит от нее линейно, т.к. в этом случае неизвестная функция T(x,t) (и все ее производные) входит в него в первой степени. Линейное уравнение теплопроводности имеет аналитическое решение, в то время, как подавляющее большинство нелинейных уравнений в частных производных можно решить только численно.

Для того, чтобы уравнения в частных производных имело единственное решение, необходимо поставить нужное количество начальных и граничных условий, т.е. соотношения типа T(x,0)=f₁(x) и T(0,t)=f₂(t). 

В качестве численных алгоритмов решения уравнений в частных производных наиболее часто используют метод сеток (разностные схемы).