12.1.1. О постановке краевых задач
12.3.1. О разностных схемах

12.3.2. Жесткие краевые задачи*

Один из случаев, когда применение разностных схем может быть очень полезным, связан с решением жестких краевых задач (подробнее о жестких ОДУ читайте в гл. 11). В частности, рассматриваемая задача о встречных световых пучках становится жесткой при увеличении коэффициента ослабления a(x) в несколько десятков раз. Например, при попытке решить ее с a(x):=100 с помощью листинга 12.2, вместо ответа выдается сообщение об ошибке "Can't converge to a solution. Encountered too many integration steps" ("Не сходится к решению. Слишком много шагов интегрирования"). Это и неудивительно, поскольку жесткие системы характерны тем, что требуют исключительно малого значения шага в стандартных алгоритмах.
Для жестких задач неприменимы и явные разностные схемы, о которых рассказывалось в предыдущем разделе. Результат расчетов по программе листинга 12.6, например с a(x):=20 (рис. 12.9), дает характерную для неустойчивых разностных схем "разболтку" - колебания нарастающей амплитуды, не имеющие ничего общего с реальным решением.

Рис. 12.9. Неверное решение жесткой краевой задачи по неустойчивой явной разностной схеме

Выходом из положения будет использование неявных разностных схем. Применительно к нашей задаче достаточно заменить правые части уравнений (1) значениями не на левой, а на правой границе каждого шага:
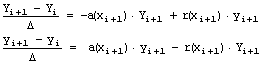(4)
Граничные условия, конечно, можно оставить в том же виде (2). Поскольку мы имеем дело с линейными дифференциальными уравнениями, то и схему (4) легко будет записать в виде матричного равенства (3), перегруппировывая соответствующим образом выражение (4) и приводя подобные слагаемые. Разумеется, полученная матрица A будет иной, нежели A матрица для явной схемы (1). Поэтому и решение (реализация неявной схемы) может отличаться от изображенного на рис. 12.9 результата расчетов по явной схеме. Программа, составленная для решения системы (4), приведена на листинге 12.7.

Листинг 12.7. Реализация неявной разностной схемы для жесткой краевой задачи
(для просмотра ссылки требуется MathCAD 2001 или браузер techexplorer компании IBM)

Не будем специально останавливаться на обсуждении листинга 12.7, поскольку он почти в точности повторяет предыдущий листинг. Отличие заключается лишь в формировании матрицы A другим способом, согласно неявной схеме. Решение, показанное на рис. 12.10, демонстрирует, что произошло небольшое чудо: "разболтка" исчезла, а распределение интенсивностей стало физически предсказуемым. Обратите внимание, что (из-за взятого нами слишком большого коэффициента ослабления излучения) отраженный пучок света имеет очень маленькую интенсивность, и ее пришлось построить на графике с увеличением в тысячу раз.

Рис. 12.10. Решение краевой задачи разностным методом (листинг 12.7)

Замечание
Все примеры, рассмотренные в этом разделе, связаны с краевыми задачами для линейных ОДУ. Благодаря линейности исходных уравнений, и система разностных уравнений получалась линейной. Если же дифференциальные уравнения нелинейные, то решение их разностным методом существенно усложняется. Разбор соответствующих Mathcad-программ выходит далеко за пределы данной книги. Но читатель, заинтересовавшийся примером найдет некоторые сведения о них на странице Нелинейные краевые задачи .