Аттракторы динамических систем

Для нахождения неподвижных точек систем ОДУ требуется (приравняв производные по времени в правых частях нулю) решить получившуюся систему алгебраических уравнений:

 

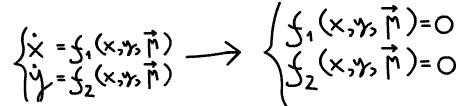
В частности, исследование зависимости фазового портрета от параметров системы ОДУ и поиск бифуркаций удобно проводить при помощи алгоритмов продолжения. Метод продолжения по параметру описан в главе, посвященной нелинейным уравнениям.

Аттракторы могут быть обычными точками в фазовом пространстве, а могут иметь более сложную топологию, являясь, к примеру, замкнутыми кривыми (т.н. предельными циклами). На основе анализа асимптотического поведения динамической системы при приближении к аттракторам, можно построить классификацию аттракторов.

Аттракторы могут быть либо устойчивыми (тогда траектории в фазовом пространстве стремятся к ним), так и неустойчивыми(тогда траектории, даже начинающиеся очень близко от особой точки, отталкиваются от нее - такие особые точки называют репеллерами). Устойчивость аттракторов можно определить путем линеаризации исходной динамической системы в малой окрестности аттрактора и исследованием свойств полученной линеаризованной системы, которая, в силу линейности, может быть решена аналитически.

 

Если динамическая система, помимо прочего, зависит от некоторого параметра m, то при изменении этого параметра фазовый портрет системы (т.е. структура аттракторов) может изменяться. Например, могут возникать новые аттракторы, старые пропадать и т.п. Такие явления называют бифуркациями, и их исследование играет чрезвычайно важную роль в исследовании динамической системы.