Неявный алгоритм "предиктор-корректор"

Схема типа "предиктор-корректор" является естественным усложнением многошаговых методов типа Адамса-Бэшфорта. Проиллюстрируем их основную идею. Для решения уравнения
 
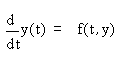
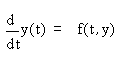
аппроксимируем его разностным аналогом (неявной схемой Эйлера) в точке y (t_n+1/2):

В эту формулу искомое y (t_n+1) входит как в левой, так и в правой части, причем в правой части от этого аргумента считается функция f(.). Иными словами, формула является (в общем случае) нелинейным уравнением с неизвестным y_n+1. Смысл схем типа "предиктор-корректор" состоит в решении такого уравнения на каждом шаге при помощи какого-либо итерационного численного алгоритма (например, Ньютона). При этом в качестве начальной итерации для решения этого уравнения берется экстраполяция зависимости y(t) в точке t_n+1 по предыдущим точкам. Эти точки известны из решения ОДУ на предыдущих шагах. К примеру, можно использовать алгоритм кубической полиномиальной экстраполяции (4-шаговый алгоритм Адамса-Бэшфорта):

Таким образом, алгоритм "предиктор-корректор" включает (на каждом шаге интегрирования ОДУ) 2 этапа (см. рис.):
1. предиктор - предсказание значения y_n+1 при помощи экстраполяции по предыдущим точкам.
2. корректор - уточнение y_n+1 посредством решения нелинейного уравнения неявной схемы итерационным методом (типа алгоритма Ньютона).